About Our Logo
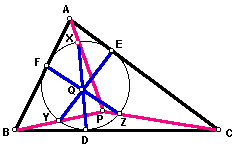 Let
P be any point inside triangle ABC as shown. Draw the lines PA, PB, and PC. These
lines meet the circle inscribed in the triangle at points X, Y, and Z, respectively.
The inscribed circle touches the sides of the triangle at points D, E, and F, as
shown. Then, no matter where point P is chosen, the lines DX, EY, and FZ will always
meet at a point (labelled Q in the figure).
Let
P be any point inside triangle ABC as shown. Draw the lines PA, PB, and PC. These
lines meet the circle inscribed in the triangle at points X, Y, and Z, respectively.
The inscribed circle touches the sides of the triangle at points D, E, and F, as
shown. Then, no matter where point P is chosen, the lines DX, EY, and FZ will always
meet at a point (labelled Q in the figure).
If you have a QuickTime Movie Viewer, you can see an animated
version of our logo (354K). This animation shows point P moving around the triangle
and you can see that lines DX, EY, and FZ remain concurrent at all times. The animation
was produced using Geometer's Sketchpad (version 2.1) and flattened with FastPlayer
(version 1.1).
There are many generalizations of this pretty result. The result was discovered
by Stanley Rabinowitz in 1990. The details
surrounding its discovery is a long story.
Reference:
Stanley Rabinowitz, "Problem 1364", Mathematics Magazine. 64(1991)60.
Return to MathPro home page.
 Let
P be any point inside triangle ABC as shown. Draw the lines PA, PB, and PC. These
lines meet the circle inscribed in the triangle at points X, Y, and Z, respectively.
The inscribed circle touches the sides of the triangle at points D, E, and F, as
shown. Then, no matter where point P is chosen, the lines DX, EY, and FZ will always
meet at a point (labelled Q in the figure).
Let
P be any point inside triangle ABC as shown. Draw the lines PA, PB, and PC. These
lines meet the circle inscribed in the triangle at points X, Y, and Z, respectively.
The inscribed circle touches the sides of the triangle at points D, E, and F, as
shown. Then, no matter where point P is chosen, the lines DX, EY, and FZ will always
meet at a point (labelled Q in the figure).