1995 Konhauser Problemfest: Results and Problems

The third annual Konhauser Problemfest, a problem-solving contest for teams from Macalester, St. Olaf, and Carleton Colleges was held on Saturday, February 25, 1995. Information about this competition has been provided by Stan Wagon (wagon@macalstr.edu) and appears here with his permission.

A noteworthy feature of this year's contest was the presentation of a Helaman Ferguson sculpture which will serve as a trophy to travel to the winning school each year. The sculpture uses 16 pieces in two colors of polished granite to illustrate a dissection proof of the pizza theorem (see Mathematics Magazine. 67(1994)267). 

Results:

 1. Carleton #1      70 pts     Daniel Martin and Neal Weiner
 2. Carleton #2      68 pts     John Costello, Curtis Mitchell, Liz Stanhope
 3. Macalester #1    58 pts     Michael Dekker, Sim Simeonov, Michael Wolfe
 4. Carleton #3      44 pts
 5. St. Olaf #1      34 pts
 6. Carleton 4       32 pts
 7. Macalester 2     25 pts
 8. Macalester 2A    25 pts
 9. St Olaf 2        16 pts
10. St Olaf 3        13 pts
Here is the complete text of the 1995 Konhauser Problemfest problems (which were selected by Stan Wagon from various places, mostly the old Konhauser files). The hardest ones from the point of view of the contest were #5, #6, #7, and #8. Wagon would have predicted that #8 was hardest, but two teams solved it. Only one team solved #6.

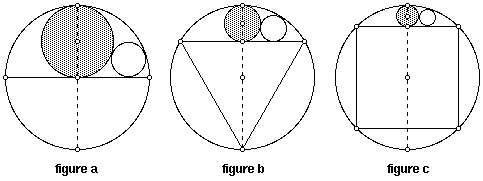
Problem 1. Circular Surprises

In the diagram, the large circle has radius one, the inscribed figures are a diameter (a), an equilateral triangle (b), and a square (c), the shaded circle is tangent to the top of the circle, and the other tangencies are as they appear. Determine the radii of the shaded and unshaded circles.

Problem 2. A Vintage Year

The year 1979 was unusual in that it results from stringing together distinct 2-digit primes, namely 19, 97, and 79. The next time this happens is in 2311, which comes from 23, 31, and 11. When will this happen for the last time? Remember: the primes must be distinct (and the examples are not meant to suggest that there are only three primes).

Problem 3. A Circular Committee

A committee with 1,995 members sits around a circular table. Every hour there is a vote and each member must vote either YES or NO. Everyone votes his or her conscience on the first round, but after that the following rule is obeyed: On the nth vote, if a person's vote is the same as at least one of the two votes of adjacent committee members, the member votes the same way on the (n+1)st round as on the nth. Otherwise the person's (n+1)st vote is the opposite of his or her nth. Prove that, regardless of the first-round votes, there will come a time after which no one's votes will change.

Problem 4. Complex Relationships

Let a, b, c, d denote complex numbers. True or False:
  1. If a + b = 0 and |a| = |b|, then a^2 = b^2.
  2. If a + b + c = 0 and |a| = |b| = |c|, then a^3 = b^3 = c^3.
  3. If a + b + c + d = 0 and |a| = |b| = |c| = |d|, then a^4 = b^4 = c^4 = d^4.

Problem 5. The Middle of a Moving Line

Suppose that L and M are two nonintersecting lines in 3-space that are perpendicular to each other. A line segment PQ of fixed length moves so that P is on L and and Q is on M. What is the locus of the midpoint of PQ?

Note: A line L in 3-space is perpendicular to another line M if M is contained in a plane perpendicular to L.

Problem 6. Visible People

Suppose n people, all having distinct heights, are standing in a single-file line. Call a person "visible" if he or she is taller than anyone in front of him or her (and so is visible to a person looking at the line from the front). Assuming a random distribution of the people into the lines, how large must n be in order that the expected number of visible people is 10?

Problem 7. Find the Pattern

The squares of an infinite chessboard are numbered as illustrated. The number 0 is placed in the lower left- hand corner; each remaining square is numbered with the smallest nonnegative integer that does not already appear to the left of it in the same row or below it in the same column. If the first row (column) is called the zeroth row (column), which number will appear in the 666th row and 401st column? 

|     |     |    |     |     |     |
----------------------------------------
|  5  |  4  |  7 |  6  |  1  |  0  |
----------------------------------------
|  4  |  5  |  6 |  7  |  0  |  1  |
----------------------------------------
|  3  |  2  |  1 |  0  |  7  |  6  |
----------------------------------------
|  2  |  3  |  0 |  1  |  6  |  7  |
----------------------------------------
|  1  |  0  |  3 |  2  |  5  |  4  |
----------------------------------------
|  0  |  1  |  2 |  3  |  4  |  5  |
----------------------------------------

Problem 8. Count the Tilings

The diagram shows a tiling of a 2x7 rectangle with 1x1 and 1x2 tiles (singletons and dominoes; dominoes may be placed horizontally or vertically). How many such tilings of a 2x7 grid are there? 
+--+-----+--+--+-----+
|  |     |  |  |     |
+--+--+--+  |  +--+--+
|     |  |  |  |  |  |
+-----+--+--+--+--+--+

Problem 9. 11111111111111...

Prove that there are infinitely many integers n for which the base-10 number obtained by stringing together n 1's is divisible by n. For example, 111 is divisible by 3.

Problem10. Three Rising Vectors

A rising vector in the plane is one whose vertical component is nonnegative. The sum of two rising vectors of length one can be very short. Prove that the sum of three rising vectors, all having length one, cannot have length less than one.

Notes:

Go to electronic publications page
Go to MathPro Press home page